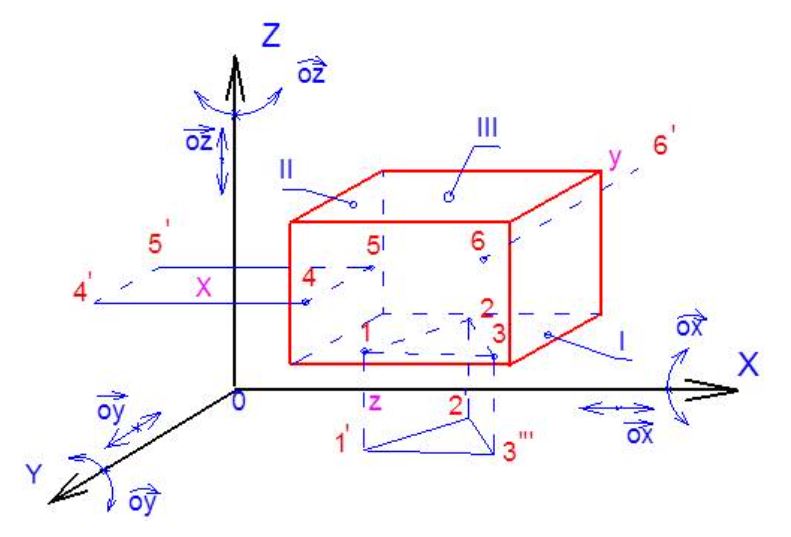
Trong bài viết về “Xây dựng hệ trục tọa độ máy đo CMM” đã đề cập tới tương quan giữa hệ trục tọa độ của dụng cụ đo và hệ trục tọa độ của vật cần đo.
NHẮC LẠI VỀ TƯƠNG QUAN TRỤC TỌA ĐỘ ĐO
Qua đó, chúng ta thấy được bản chất đo kích thước chính là tìm tọa độ của các điểm đo (đối tượng cần đo) trong hệ quy chiếu của dụng cụ đo. Hệ quy chiếu của dụng cụ đo được gọi là chuẩn tham chiếu.
Để đo được kích thước của vật theo hệ quy chiếu được chỉ định trong bản vẽ (Gốc kích thước, phương chiếu). Cần phải xây dựng tương quan giữa hệ trục của dụng cụ đo với hệ trục của vật cần đo.
Các dụng cụ đo cơ bản như thước kẹp, panme, thước đo cao độ… đều là các dụng cụ đo có hệ trục cố định là thân thước với vạch chia kích thước, hoặc bản thân kích thước của dụng cụ đo như đường kính, chiều dày… Khi sử dụng các dụng cụ đo này, thông thường chúng ta sẽ di chuyển dụng cụ đo hoặc vật cần đo để điều chỉnh mối tương quan hệ trục này.
Với các dụng cụ đo dạng dưỡng đo như Pin gauge, Block gauge, Thickness… không thể hiện rõ yếu tố tọa độ điểm đo. Tuy nhiên để có kết quả đo chính xác, vẫn phải đảm bảo các tương quan giữa dụng cụ đo và vật đo như hướng đo. Hệ quy chiếu của dụng cụ đo trong trường hợp này chính là kích thước dưỡng đo như đường kính PIN đo, chiều dày Block đo, … và kết quả thu được là GIỐNG (bằng kích thước dưỡng đo) hay KHÁC (khác kích thước dưỡng đo). Các dụng cụ đo chuyên dụng khác mình không hiểu rõ bản chất nên chỉ đề cập tới phạm vi các dụng cụ đo cơ bản. Bài viết nhằm hướng tới giải thích và làm quen với yếu tố “tọa độ” trước khi đi vào nội dung liên quan đến máy đo tọa độ 3 chiều CMM.
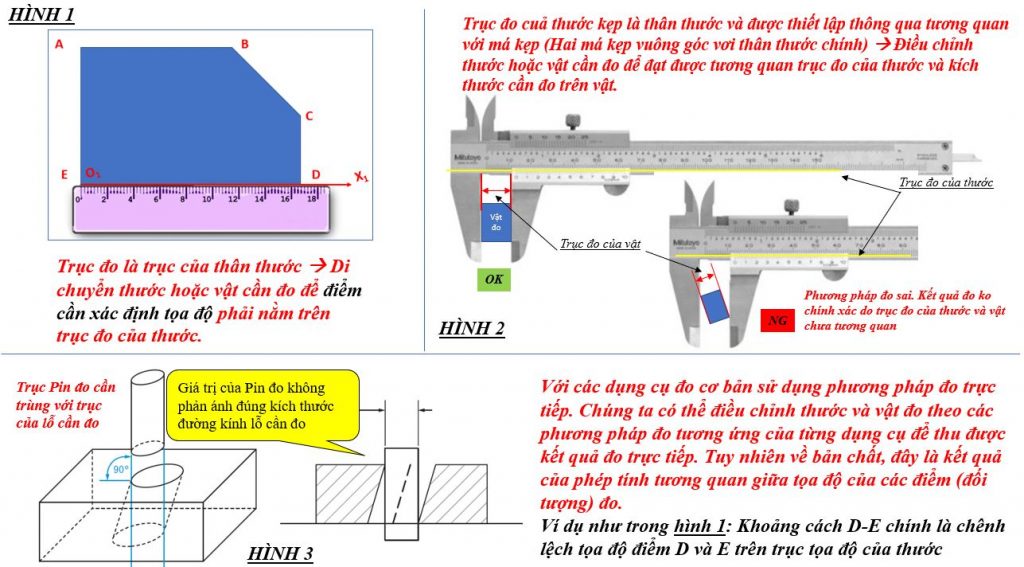
Với các dụng cụ đo cơ bản sử dụng phương pháp đo trực tiếp. Chúng ta có thể điều chỉnh thước và vật đo theo các phương pháp đo tương ứng của từng dụng cụ để thu được kết quả đo trực tiếp. Tuy nhiên về bản chất, đây là kết quả của phép tính tương quan giữa tọa độ của các điểm (đối tượng) đo trong hệ trục của dụng cụ đo. Ví dụ như trong Hình 1 của ảnh minh họa phía trên hoặc với dụng cụ đo chiều cao như dưới đây.

SỐ CHIỀU CỦA DỤNG CỤ ĐO (2D, 2.5D, 3D…)
Chúng ta thường nghe nói đến máy đo (dụng cụ đo) 2D, 2.5D, 3D. Hay nói cách khác là dụng cụ đo 3 chiều, 2 chiều, 2.5 chiều (máy đo 2 chiều tích hợp thêm đầu đo của một chiều còn lại, tuy nhiên chỉ đo được các kích thước đơn giản thì được coi là cộng thêm 0.5D và gọi là 2.5D). (Nội dung bài viết thể hiện quan điểm cá nhân và mục đích để chia sẻ những gì tác giả hiểu về lĩnh vực đo kích thước, do vậy nếu có quan điểm khác về nhóm dụng cụ đo thì mọi người có thể comment và chia sẻ dưới mục bình luận).
Bản chất chiều đo ở đây chính là hệ trục tọa độ đo.
- Hệ trục OXY (hay nói cách khác là tọa độ điểm đo hay đối tượng đo được chiếu lên mặt phẳng OXY). Tọa độ điểm đo (đối tượng đo) được thể hiện qua đại lượng X, Y so với gốc tham chiếu O ở trong hệ trục tọa độ đo OXY.
- Hệ trục tọa độ OXYZ. Tọa độ điểm đo (đối tượng đo) được thể hiện qua 3 đại lượng trong không gian 3 chiều là X, Y, Z so với gốc tham chiếu O ở trong hệ trục tọa độ này.
Vậy câu hỏi đặt ra là, các dụng cụ đo cơ bản thuộc nhóm nào? (2D, 2.5D hay 3D?). Theo tôi, các dụng cụ đo như thước kẹp, panme, high gauge… sẽ thuộc nhóm … 1D. Vì bản chất kích thước đo được phản ánh qua 1 trục tọa độ duy nhất là thân (trục) thước đo.
Một số máy đo chuyên dụng cho một mục đích hoặc một loại sản phẩm như máy đo trục (roller system), máy đo ăn khớp bánh răng (Gear roller system) hay máy đo biên dạng bánh rang thì tôi cũng không biết nên đặt chúng chính xác ở nhóm nào. Tuy nhiên chúng ta cứ hiểu rằng kết quả đo được tính toán trên kết quả đo của từng điểm đo hay nói cách khác là tọa độ của từng điểm đo. Vậy tọa độ điểm đo được dụng cụ đo thể hiện qua mấy thông số thì đó được coi là số chiều của dụng cụ đo có thể kiểm soát được.
CÁC YẾU TỐ XÁC ĐỊNH HỆ TRỤC TỌA ĐỘ ĐO
Hệ trục tọa độ đo là chuẩn tham chiếu để tính toán kết quả đo dựa trên tọa độ của các điểm đo (đối tượng đo). Với các dụng cụ đo cơ bản, chúng ta có thể dịch chuyển hệ trục tọa độ bằng cách di chuyển thước và vật đo. Thiết kế của dụng cụ đo và nguyên lý đo phù hợp với phương pháp đo này.
Tuy nhiên với máy đo. Việc di chuyển dụng cụ đo và vật trong quá trình đo là rất hạn chế thậm chí là không thể. Khi đó vật đo thường được cố định bằng Jig (dụng cụ gá kẹp) trên bàn đo và có thể máy đo tích hợp chức năng xoay mâm gá. Quá trình đo được tiến hành dựa trên việc di chuyển đầu do và xoay mâm gá.
Để thu được kết quả đo phản ánh đúng theo yêu cầu của bản vẽ (hay nói cách khác là hệ trục tọa độ của vật đo được chỉ định trong bản vẽ) cần phải có bước xây dựng hệ trục tọa độ. Đây chính là bước căn chỉnh hệ trục tọa độ của máy đo cho khớp với hệ trục của vật bằng một loạt các phép rời hệ trục tọa độ như tịnh tiến và xoay.
Muốn xây dựng được hệ trục này, cần phải nắm được yếu tố nào dùng để dựng lên (xác định) một hệ trục tọa độ duy nhất.
3 yếu tố xác định một hệ tọa độ duy nhất đó là.
- Mặt phẳng tham chiếu
- Trục tham chiếu (thuộc mặt phẳng tham chiếu)
- Gốc tham chiếu (của trục tham chiếu)
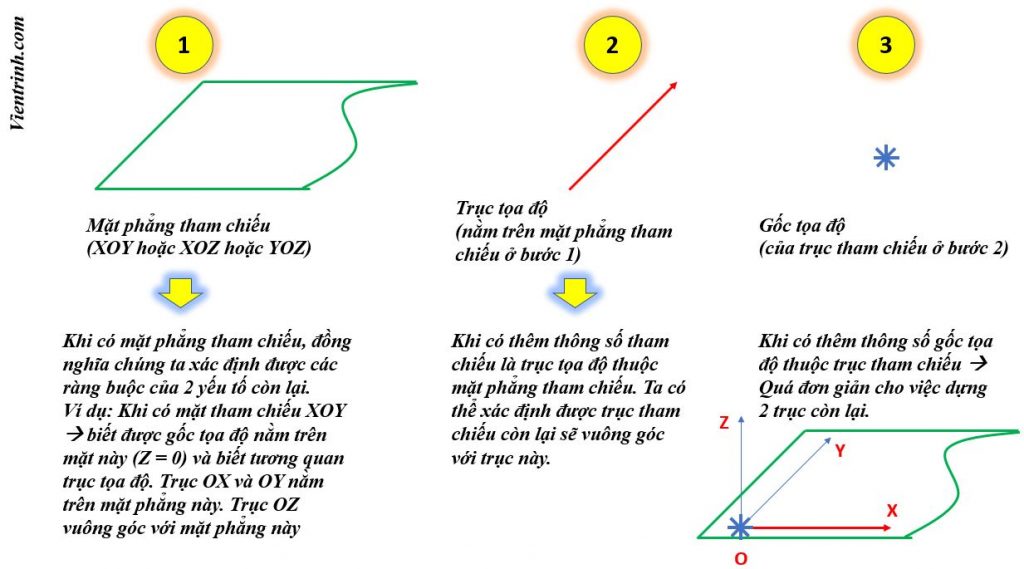
Lưu ý, 3 yếu tố này có sự ràng buộc. Trục tham chiếu là một trong 2 trục nằm trên mặt phẳng tham chiếu. Gốc tham chiếu là gốc nằm trên trục tham chiếu. Sự ràng buộc này nhằm đảm bảo tính toàn vẹn của hệ trục tọa độ.Nếu không hiểu rõ, khi xây dựng hệ trục, các bạn rất dễ tạo ra một hệ trục tọa độ không đúng theo yêu cầu bản thiết kế. Có thể sự sai khác này rất nhỏ, nhưng về bản chất thì hệ tọa độ đó là khác biệt so với hệ tọa độ cần thiết lập.
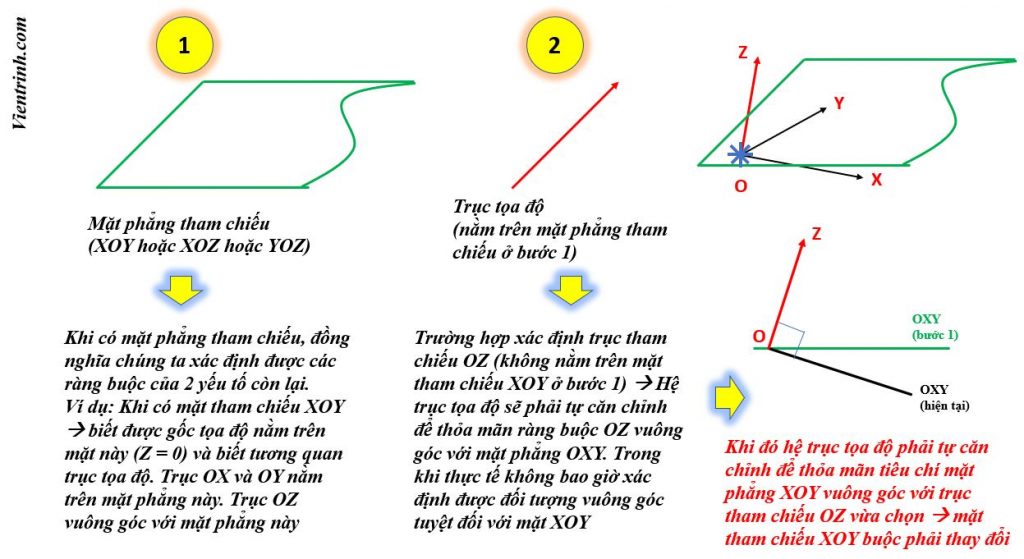
Đến đây có thể bạn nghĩ rằng yếu tố xác định hệ trục tọa độ này phù hợp với không gian tọa độ OXYZ, và sẽ băn khoăn với trường hợp đo 2D thì yếu tố xác định là gì.
Thực ra 3D chỉ khác biệt ở 1 chiều (trục tọa độ) so với 2D, và trục tọa độ này hoàn toàn được xác định khi có hệ trục tọa độ 2D. (vuông góc với mặt phẳng tham chiếu 2D, đi qua gốc tọa độ, hướng của trục hay còn gọi là chiều của vector chỉ phương sẽ tuân theo quy tắc tam diện thuận). Các bạn có thể tra cứu thêm trên để hiểu các thuật ngữ như vector chỉ phương, tam diện thuân. (Đây là các kiến thức khá cơ bản khi học hình học không gian).
LỜI KẾT
Để xây dựng được hệ trục tọa độ cho máy đo CMM, chúng ta cần xác định được 3 yếu tố tương quan
- Mặt phẳng tham chiếu
- Trục tham chiếu (thuộc mặt phẳng tham chiếu)
- Gốc tham chiếu (của trục tham chiếu).
Nếu để ý kỹ, bạn sẽ thấy các yếu tố tương đương với việc định vị 6 bậc tự do trong gia công cơ khí.
- Mặt phẳng tham chiếu → Định vị 3 bậc tự do (1,2,3)
- Trục tham chiếu → Định vị 2 bậc tự đo (4,5)
- Gốc tham chiếu → Định vị bậc còn lại (6)
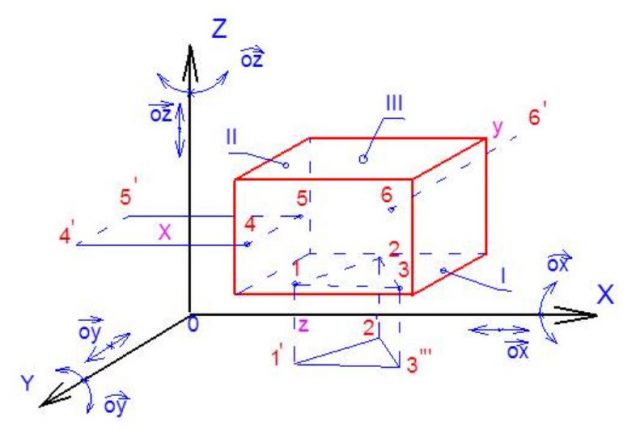
Nguyên tắc này chỉ ra rằng, muốn một vật có vị trí xác định trong không gian 3 chiều, cần phải khống chế hay nói cách khác là xác định được 6 bậc tự do của vật đó.
Vậy để đo được một vật bằng máy đo tọa độ 3 chiều, chúng ta cũng cần phải xác định được vị trí của vật trong không gian 3 chiều (hệ tọa độ) của máy.
Để đo được kích thước theo hệ quy chiếu của vật, cần xây dựng hệ trục tọa độ hay nói cách khác là dùng các phép dựng hình để di chuyển (alignment) hệ trục tọa độ của máy về hệ trục tọa độ của vật.
Bài viết tiếp theo sẽ đề cập tới các phương pháp dựng hệ trục tọa độ PCS từ hệ trục MCS qua các phép dựng trục cơ bản (tịnh tiến và xoay)